an unusual java class

I was reading a forum thread in www.daniweb.com where someone was asking if there is any way to pick what method to run on run time rather than specifying what method to run during development. I have thought of the same problem before, and I decided to see if this is possible by trying to actually build a class that does this. Here is the code:


import javax.swing.*;

public class MixTapes{

public static void main(String[] args){
int s = 0;
while(s != -1){
s = new Integer(JOptionPane.showInputDialog("pick method:\n1 fo method1\n2 for method2\n25 for method25\n-1 for quiting")).intValue();
pickWhichMethodToRun(s);
}

}

public static void method1(){
System.out.println("First method has been chosen");
}

public static void method2(){
System.out.println("Second method has been chosen");
}

public static void method25(){
System.out.println("Twenty-fifth method has been chosen");
}
public static void pickWhichMethodToRun(int s){

switch(s){
case 1:
method1();
break;

case 2:
method2();
break;

case 25:
method25();
break;

default:
System.out.println("haven't picked an existing method");
}

}

}


od command in Linux and a class in Java

Because of my strong desire to earn LPI certification (Linux Professional Institute Certification), in between my studies, I also read the LPIC-1 Linux Guide. Today I was working on the od command in Linux. It is not hard to type od filename and see what it returns, but I was having a hard time to understand what exactly was going on so I started to convert numbers from base eight to ten and then to base two (I know… I could just convert them to base two directly :P) to see what was going on, but I was making calculation mistakes, and since I also like coding, I thought I’d build a Java class that does conversions for me and make my studying od easier. Read on for what od actually does, and for the code in Java.

od stands for octal dump. If one just types in a terminal od filename, the output is a nine column retsult of numbers in base eight. The first column indicates the bytes represented in that row. for example, column one in row 1 will output 0000000 and row two, column one will output 0000020. To understand what this means, lets first convert 0000020 to decimal, getting 16. Now, the 0000000 and 0000020 indicate that columns two to nine in row one contain bytes one through 16. Now one might ask: if there are 16 bytes represented, why only eight columns (excluding the first)? Well, every two bytes are combined to give one octal number. Say for example you have bytes AB, and you pass this content to od command. the output will be :
0000000 041101 000012
0000003
If one converts 041101 into binary, the result is:
0 100 001 001 000 001, which equals the following two bytes:
01000010 01000001, which then equal the ACII, binary, values of characters A and B.
The 000012, will be output even if od is passed no text at all. I looked up the ASCII table, and found out that octal 000012 (decimal ten) is the value of new line character. So, seems like od assumes that every file, even an empty one ends with a new line character, so it outputs either 000012 or what it gets after combining this byte with another (in case the number of bytes in a file is odd, else, 000012 is not combined with any other byte and is output as is).

UPDATE: The 0000012 ASCII values is actually the form feed character. More on that in the following Wikipedia link.

The number 0000003 in column one, row two, in this case, indicates that there are three bytes shown in the previous row. Note that each row has at most nine columns. If there are no bytes to fill all nine columns of a row, the row will have less columns.

Now, the od command may be passed parameters to output decimal ASCII values of each byte separately (od -t dC filename), or hexadecimal values obtained by combining two consecutive bytes (od -x filename). There are other options that may be passed to od command, but the logic behind it is explained here, I believe.

As far as the code in Java goes, I will only copy paste the code. The comments in it are sufficiently explanatory:


import java.util.*;
import javax.swing.*;

public class ConvertNumber{

public static void main(String[] args){
//this line of code prompts a user to specify the method they want to use
String met = JOptionPane.showInputDialog("which method do you need:\ndecToAny(type d), or the method\nto convert a number with a lower base to decimal(type td)").toUpperCase();

//this block of code is executed if the user wants to run the method that generates a decmial numbers representation
//in a base lower than ten
if(met.equals("D")){
String s = JOptionPane.showInputDialog("type in the decimal number and the base you want it converted to with a comma in between (type dec-num, new-base (new base should be lower than ten greater than 1))");
StringTokenizer st = new StringTokenizer(s, ",");
int x = new Integer(st.nextToken().trim()).intValue();
int y = new Integer(st.nextToken().trim()).intValue();

System.out.println(decToAny(x, y));
}

//this block of code is executed if the user wants a number converted to base ten
if(met.equals("TD")){
String s = JOptionPane.showInputDialog("give the number and the base it is in with a comma in between (num,base)");
StringTokenizer str = new StringTokenizer(s, ",");
int num = new Integer(str.nextToken().trim()).intValue();
int b = new Integer(str.nextToken().trim()).intValue();
System.out.println(toDec(num, b));
}
}

public static String decToAny(int x, int baza){
String rez = "";
//this method converts a number that's in base ten to a base lower than ten and greater than two
//the number to convert is x and the base to which to convert is baza
//the result is a string. all one needs to do to convert it to int is the "new Integer(rez).intValue()" line
while(x > 0){
rez = x%baza + rez;
x = x/baza;
}

return rez;
}

//this method converts a number x in base baza into a decimal number
public static int toDec(int x, int baza){
int rez = 0;
int lim = ("" + x).length();
for(int i = 0; i < lim; i++){
//this line converts number x to string. it then iterates through that string from character
//at position 0 to the last and converts the character back to int and multiplies it with
//base raised to the power indicated by lim - i - 1 (lim is the number of digits in the number)
//since character at position zero is raised to a power that is less than the number od digits by one
//you get that from the following lim - i - 1.
rez = new Integer("" + ("" + x).charAt(i)).intValue() * (int)Math.pow(baza, lim - i - 1) + rez;
}
return rez;

}

}


If there is anything you would want me to add or clarify further as far as anything related here goes, please comment with the question you would want me to tackle. I will study it, and will make a post for it.

elementary transformations on a matrix

The following is a complete class with a method for performing elementary transformations on any matrix, regardless of the number of rows and columns. It is written in Java. All explanations are given preceding each method.

I copied and tried the code from my blog, and realized that:

WordPress will change quotes into some other character, so if you copy the code, you will have to replace what you get for quotes with actual quotes.

Same for minus (-) sign. Just replace what you get with the actual – character.

Somewhere in the line 93 or so, you should have k–, which WordPress turns into k-. Change that too, and this class should work fine.

I also left a main method inside. I used that to test my code while I wrote it. Hope this is of any help to you.

CODE STARTS WITH THE NEXT LINE

import javax.swing.*;

public class ElementaryTransformations{

public static void main(String[] args){
int x = new Integer(JOptionPane.showInputDialog(“Rendi i matrices?”)).intValue();
int[][] y = GetMatrix(x, x + 1);
y = SwitchRows(y, x, 2);
ShowMatrix(y);
System.out.println();
ShowMatrix(Transform(y));
}
//this method gets the matrix from a user. the matrix will have x rows, and y cols
public static int[][] GetMatrix(int x, int y){
int[][] rez = new int[x][y];
for(int i = 0; i < x; i++){
for(int j = 0; j < y; j++){
rez[i][j] = new Integer(JOptionPane.showInputDialog(“Ama vleren e elementit ” + i + “,” + j)).intValue();
}
}
return rez;
}
//this method makes a matrix appear in a console
public static void ShowMatrix(int[][] x){
for(int i = 0; i < x.length; i++){
for(int j = 0; j < x[0].length; j++){
System.out.print(x[i][j] + ” “);
}
System.out.println();
}
}

//this method switches positions of two rows. it puts a row ‘a’ in position ‘b’
//and row ‘b’ in position ‘a’
//when using this method, the first row is row 1, not 0, and the last row is
//x.length instead of x.length – 1.
public static int[][] SwitchRows(int[][] x, int a, int b){
int[][] rez = x;
//this if statment orders variables a and b by magnitude
//because of the way the method is written, if a is greater than b
//the method won’t work.
if(a > b){
int temp = a;
a = b;
b = temp;
}
int[][] temp = new int[x.length + 1][x[0].length];
//these two for statments build a temporary double array, out of the
//array given to the method. the row a is copied in position a and a+1
//thus, temp array has one row more than the original array (matrix)
for(int i = 0; i < x.length + 1; i++){
for(int j = 0; j < x[0].length; j++){
if(i < a){
temp[i][j] = rez[i][j];
}
if(i >= a){
temp[i][j] = rez[i – 1][j];
}
}
}
//these two for loops copy the temp matrix into rez matrix, putting row ‘b’
//in position ‘a’ and putting row ‘a’ in position ‘b’
for(int i = 0; i < x.length; i++){
for(int j = 0; j < x[0].length; j++){
if(i == a – 1){
rez[i][j] = temp[b][j];
}
if(i == b – 1){
rez[i][j] = temp[a][j];
}
}
}
return rez;
}
//this is the method that performs elementary transformations on the given matrix x
//elementary transformations continue until all matrix elements below the main diagonal
//equal zero
//(main diagonal is the one from upper left to lower right corner)
public static int[][] Transform(int[][] x){
int[][] rez = x;
for(int i = 0; i < rez.length; i++){
if(rez[i][i] == 0){
if(NonZeroRowthisCol(rez, i, i) != -1){
SwitchRows(rez, i, NonZeroRowthisCol(rez, i, i));
}
}
if(rez[i][i] != 0){
for(int j = i + 1; j < rez.length; j++){
//this part is tricky; if we start with k = i, and proceed all the way
//up to when k = rez[0].length… rez[j][k] will first turn into zero
//(that is our purpose) and as a result, all elements in row j, except the first, will be
//multiplied with rez[i][i] and reduced by zero
//(rez[j][i] = 0 => rez[j][i]*rez[i][k] = 0 => rez[j][k]*rez[i][i] – rez[j][i]*rez[i][k] = rez[j][k]*rez[i][i] – 0)
//yielding an inacurate result. so, what we need to do is to turn rez[j][i] into zero, after we
//update elements in other columns along j row
for(int k = rez[0].length – 1; k >= i; k–){
rez[j][k] = rez[j][k]*rez[i][i] – rez[j][i]*rez[i][k];
}
}
}
}
return rez;
}//this method finds a row ‘i’ that is lower than row ‘m’ and has a nonzero
//element in column ‘n’
//as a result, this method returns ‘i’, which reprezents the position of such a row
public static int NonZeroRowthisCol(int[][] x, int m, int n){
int rez = -1;
for(int i = m + 1; i < x.length; i++){
if(x[i][n] != 0){
rez = i;
}
}
return rez;
}

CODE ENDS WITH THE LAST CURLY BRACKET

a method for generating permutations

the following are three methods that together work to generate all permutations for any number of distinct elements. Before I give the code, though, I need to explain a few things:

1. a method that calculates n!
2. a helper method, that I named ExpandString
3. the method that generates all permutations.

why ExpandString
Simple. Say we have a set with a single element. The number of permutations possible with that element is 1!, and the permutation is “a”.

Now, think of a set with two elements, namely a and be. We know that the number of permutations with one element is one, and that the permutation is “a” (that one element). Then, to generate all the permutations with two elements, you expand the string that represents the permutation with one element (“a”) in such a manner that you once add the second element at the end of it, and once at the beginning of it. As a result, you get two permutations, “ab” and “ba”.

if you’re to generate in this way permutations with three elements, you increase the number of permutations with two elements multiplying it with three and get six. Then, form six strings such that the first is “ab”, the second “ba”, the third “ab”, the fourth “ba”, the fifth “ab”, the sixth “ba”. Finally, you expand each string in such a manner that you add the third element, say c, in the first and second string at the end, in the third and fourth string in between the two letters forming the strings, and in the fifth and sixth strings, add c in the beginning of each string. As a result, you are sure you got all six distinct permutations. In the same way, one can generate all permutations for any n (natural number) elements.

note however, that ExpandString generates ONE permutation, while permute method generates ALL distinct permutations making use of ExpandString.

PERMUTATION METHOD

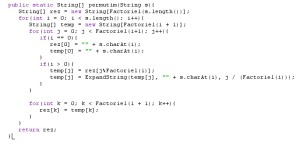
UPDATE: I can’t make the actual permutim method show correctly. somehow, wordpress removes my if statments, and the resulting code won’t work. so, I made a picture with the code, and put it inside the post. if you click on the picture, you’ll be able to see the code perfectly well.

FACTORIAL METHOD

public static int Factoriel(int x){
int rez = 1;
for(int i = 2; i<= x; i++){
rez = rez*i;
}
return rez;
}

ExpandString METHOD
public static String ExpandString(String x, String y, int z){
String rez = "";
rez = x.substring(0, z) + y + x.substring(z);
return rez;

}

Maybe more explanations are needed, but time won’t permit this time. any question though, will be answered.

Java code for transposing a matrix

Alright. This time I have some code written in Java. What it does is transposing a matrix. The code contains as follows:

class Matrica{

public static void main(String[] args){
int a = new Integer(JOptionPane.showInputDialog(“Number of rows?”)).intValue();
int b = new Integer(JOptionPane.showInputDialog(“Number of columns?”)).intValue();
int[][] y = new int[a][b];
for(int i =0; i< a; i++){
for(int j = 0; j< b; j++){
y[i][j] = new Integer(JOptionPane.showInputDialog(“Element in position “ + i + ” , “ + j)).intValue();
}
}

 

int[][] d = Transpono(y);

 

for(int x = 0; x< d.length; x++){
for(int yx = 0; yx< d[0].length; yx++){
System.out.print(d[x][yx] + ” “);
}
System.out.println();
}
}

 

public static int[][] Transpono(int[][] x){

 

int[][] answer = new int[x[0].length][x.length];

 

for(int i = 0; i <x[0].length; i++){
for(int j = 0; j < x.length; j++){
answer[i][j] = x[j][i];
}
}

 

return answer;
}

P.S. I have tested the code, so I know it works fine.

}